Match
The Xtrack Line class provides a match method that allows using a numerical optimizer to adjust knobs attached to the line in order to obtain desired values in the twiss results (or as a result of other user-defined actions).
Basic usage
The numerical optimizer can be used calling the method xtrack.Line.match().
The optimization is define by a set of Vary and Target objects defining the
knobs to be varied and the targets to be matched. Arguments not specific of the
match method are automatically dispatched to the underlying twiss calls.
The following example shows how to match the tunes and chromaticities of a ring.
import xtrack as xt
# Load a line and build a tracker
line = xt.Line.from_json('../../test_data/hllhc15_thick/lhc_thick_with_knobs.json')
line.build_tracker()
# Match tunes and chromaticities to assigned values
opt = line.match(
method='4d', # <- passed to twiss
vary=[
xt.VaryList(['kqtf.b1', 'kqtd.b1'], step=1e-8, tag='quad'),
xt.VaryList(['ksf.b1', 'ksd.b1'], step=1e-4, limits=[-0.1, 0.1], tag='sext'),
],
targets = [
xt.TargetSet(qx=62.315, qy=60.325, tol=1e-6, tag='tune'),
xt.TargetSet(dqx=10.0, dqy=12.0, tol=0.01, tag='chrom'),
])
# Inspect optimization log
opt.log()
# prints:
#
# Table: 3 rows, 18 cols
# iteration penalty alpha tag tol_met target_active hit_limits vary_active vary_0 ...
# 0 12.9073 -1 nnnn yyyy nnnn yyyy 0
# 1 0.00270443 0 nnyy yyyy nnnn yyyy 4.2729e-05
# 2 1.22005e-06 0 yyyy yyyy nnnn yyyy 4.27163e-05
# Inspect optimization outcome
opt.target_status()
opt.vary_status()
# prints:
#
# Target status:
# id state tag tol_met residue current_val target_val description
# 0 ON tune True 8.53717e-11 62.315 62.315 'qx', val=62.315, tol=1e-06, weight=10)
# 1 ON tune True 1.49214e-13 60.325 60.325 'qy', val=60.325, tol=1e-06, weight=10)
# 2 ON chrom True 1.22005e-06 10 10 'dqx', val=10, tol=0.01, weight=1)
# 3 ON chrom True -1.87538e-09 12 12 'dqy', val=12, tol=0.01, weight=1)
# Vary status:
# id state tag name lower_limit current_val upper_limit val_at_iter_0 step weight
# 0 ON quad kqtf.b1 None 4.27163e-05 None 0 1e-08 1
# 1 ON quad kqtd.b1 None -4.27199e-05 None 0 1e-08 1
# 2 ON sext ksf.b1 -0.1 0.0118965 0.1 0 0.0001 1
# 3 ON sext ksd.b1 -0.1 -0.0232137 0.1 0 0.0001 1
# Get knob values after optimization
knobs_after_match = opt.get_knob_values()
# contains: {'kqtf.b1': 4.27163e-05, 'kqtd.b1': -4.27199e-05,
# 'ksf.b1': 0.0118965, 'ksd.b1': -0.0232137}
# Get knob values before optimization
knobs_before_match = opt.get_knob_values(iteration=0)
# contains: {'kqtf.b1': 0, 'kqtd.b1': 0, 'ksf.b1': 0, 'ksd.b1': 0}
# Complete source: xtrack/examples/match/000_match_basic.py
Match at specific locations
See also xtrack.Line.match()
The match method can also be used on a portion of a beam line and/or with
targets at specific locations. By default the provided boundary conditions are
imposed at the start of the specified range. The constants xt.START and
xt.END can be used to specify targets at the start and end of the range
respectively. This is illustrated in the following example, showing how to
match a closed orbit bump in a given beamline range.
import xtrack as xt
# Load a line and build a tracker
line = xt.Line.from_json('../../test_data/hllhc15_thick/lhc_thick_with_knobs.json')
line.build_tracker()
opt = line.match(
start='mq.30l8.b1', end='mq.23l8.b1',
betx=1, bety=1, y=0, py=0, # <-- conditions at start
vary=xt.VaryList(['acbv30.l8b1', 'acbv28.l8b1', 'acbv26.l8b1', 'acbv24.l8b1'],
step=1e-10, limits=[-1e-3, 1e-3]),
targets = [
xt.TargetSet(y=3e-3, py=0, at='mb.b28l8.b1'),
xt.TargetSet(y=0, py=0, at=xt.END)
])
opt.target_status()
# prints:
#
# Target status:
# id state tag tol_met residue current_val target_val description
# 0 ON True 1.30104e-18 0.003 0.003 ('y', 'mb.b28l8.b1'), val=0.003, tol=1e- ...
# 1 ON True -3.38813e-20 -3.38813e-20 0 ('py', 'mb.b28l8.b1'), val=0, tol=1e-10, ...
# 2 ON True -4.127e-17 -4.127e-17 0 ('y', 'mq.23l8.b1'), val=0, tol=1e-10, w ...
# 3 ON True -6.1664e-19 -6.1664e-19 0 ('py', 'mq.23l8.b1'), val=0, tol=1e-10, ...
# Complete source: xtrack/examples/match/002_match_bump_basic.py
Alternatively, the boundary conditions can be imposed at the end or within the specified range as illustrated in the following examples.
import xtrack as xt
# Load a line and build a tracker
line = xt.Line.from_json('../../test_data/hllhc15_thick/lhc_thick_with_knobs.json')
line.build_tracker()
opt = line.match(
start='mq.30l8.b1', end='mq.23l8.b1',
init_at=xt.END, betx=1, bety=1, y=0, py=0, # <-- conditions at end
vary=xt.VaryList(['acbv30.l8b1', 'acbv28.l8b1', 'acbv26.l8b1', 'acbv24.l8b1'],
step=1e-10, limits=[-1e-3, 1e-3]),
targets = [
xt.TargetSet(y=3e-3, py=0, at='mb.b28l8.b1'),
xt.TargetSet(y=0, py=0, at=xt.START)
])
opt.target_status()
# prints:
#
# Target status:
# id state tag tol_met residue current_val target_val description
# 0 ON True 1.30104e-18 0.003 0.003 ('y', 'mb.b28l8.b1'), val=0.003, tol=1e- ...
# 1 ON True -3.38813e-20 -3.38813e-20 0 ('py', 'mb.b28l8.b1'), val=0, tol=1e-10, ...
# 2 ON True -4.127e-17 -4.127e-17 0 ('y', 'mq.23l8.b1'), val=0, tol=1e-10, w ...
# 3 ON True -6.1664e-19 -6.1664e-19 0 ('py', 'mq.23l8.b1'), val=0, tol=1e-10, ...
# Complete source: xtrack/examples/match/002a_match_bump_init_end.py
import xtrack as xt
# Load a line and build a tracker
line = xt.Line.from_json('../../test_data/hllhc15_thick/lhc_thick_with_knobs.json')
line.build_tracker()
opt = line.match(
start='mq.30l8.b1', end='mq.23l8.b1',
init_at='mb.b28l8.b1', betx=1, bety=1, y=3e-3, py=0, # <-- conditions at point inside the range
vary=xt.VaryList(['acbv30.l8b1', 'acbv28.l8b1', 'acbv26.l8b1', 'acbv24.l8b1'],
step=1e-10, limits=[-1e-3, 1e-3]),
targets = [
xt.TargetSet(y=0, py=0, at=xt.START),
xt.TargetSet(y=0, py=0, at=xt.END)
])
opt.target_status()
# prints:
#
# Target status:
# id state tag tol_met residue current_val target_val description
# 0 ON True -5.68188e-18 -5.68188e-18 0 ('y', 'mq.30l8.b1'), val=0, tol=1e-10, w ...
# 1 ON True -8.0272e-20 -8.0272e-20 0 ('py', 'mq.30l8.b1'), val=0, tol=1e-10, ...
# 2 ON True 1.03651e-18 1.03651e-18 0 ('y', 'mq.23l8.b1'), val=0, tol=1e-10, w ...
# 3 ON True -9.48677e-20 -9.48677e-20 0 ('py', 'mq.23l8.b1'), val=0, tol=1e-10, ...
# Complete source: xtrack/examples/match/002b_match_bump_init_middle.py
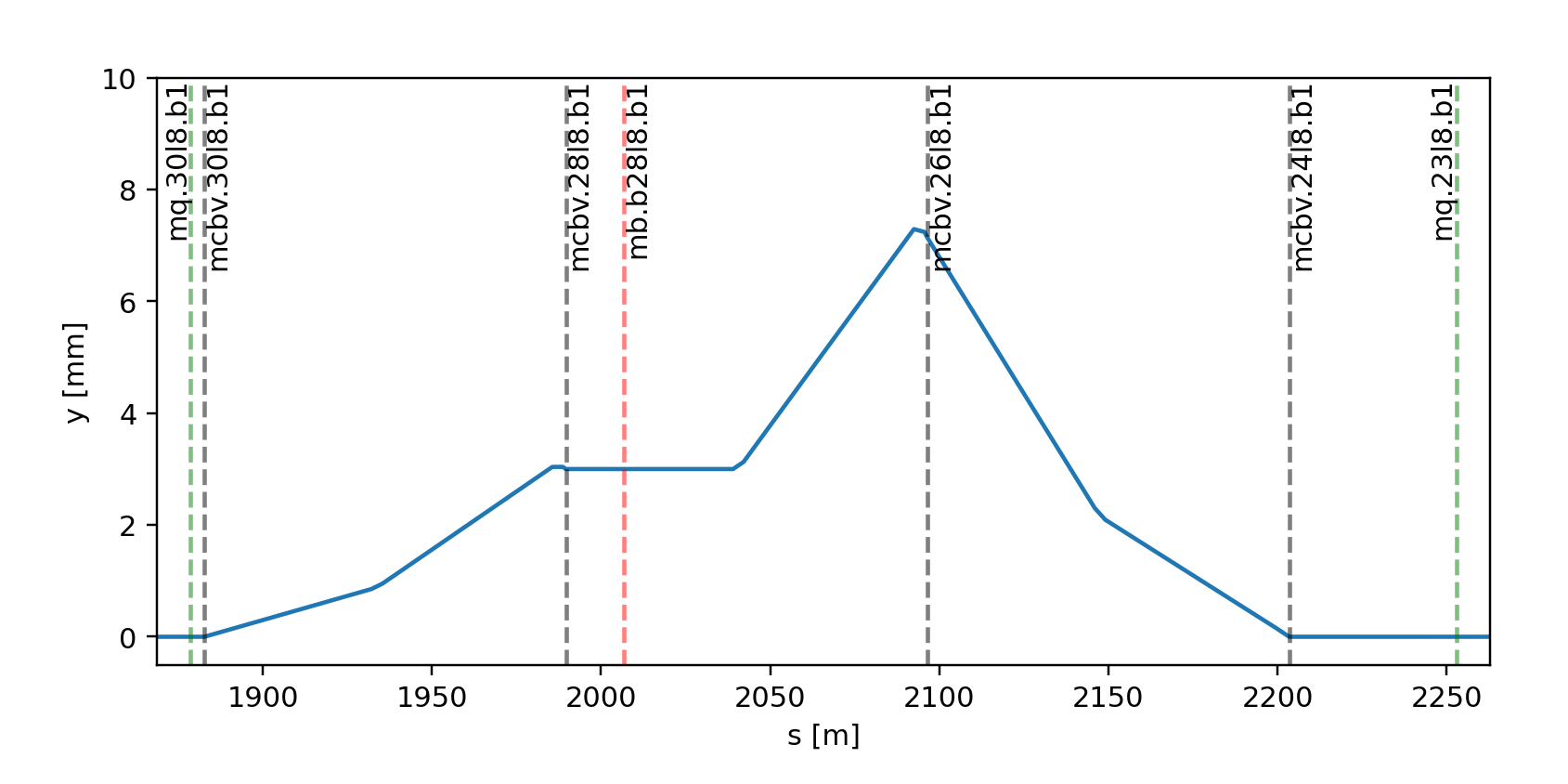
The orbit bump from the three examples above.
Boundary conditions and target values from existing table
See also xtrack.Line.match()
Boundary conditions and target values used for the matching can be obtained also from an existing TwissTable object, as illustrated in the following example.
import xtrack as xt
# Load a line and build a tracker
line = xt.Line.from_json('../../test_data/hllhc15_thick/lhc_thick_with_knobs.json')
line.build_tracker()
tw0 = line.twiss(method='4d')
opt = line.match(
start='mq.30l8.b1', end='mq.23l8.b1',
init=tw0, init_at=xt.END, # <-- Boundary conditions from table
vary=xt.VaryList(['acbv30.l8b1', 'acbv28.l8b1', 'acbv26.l8b1', 'acbv24.l8b1'],
step=1e-10, limits=[-1e-3, 1e-3]),
targets = [
xt.TargetSet(y=3e-3, py=0, at='mb.b28l8.b1'),
xt.TargetSet(['y', 'py'], value=tw0, at=xt.START) # <-- Target from table
])
opt.target_status()
# prints:
#
# Target status:
# id state tag tol_met residue current_val target_val description
# 0 ON True 1.30104e-18 0.003 0.003 ('y', 'mb.b28l8.b1'), val=0.003, tol=1e- ...
# 1 ON True -3.38813e-20 -3.38813e-20 0 ('py', 'mb.b28l8.b1'), val=0, tol=1e-10, ...
# 2 ON True -4.127e-17 -4.127e-17 0 ('y', 'mq.23l8.b1'), val=0, tol=1e-10, w ...
# 3 ON True -6.1664e-19 -6.1664e-19 0 ('py', 'mq.23l8.b1'), val=0, tol=1e-10, ...
# Complete source: xtrack/examples/match/003_match_bump_from_table.py
Match involving multiple lines
See also xtrack.Line.match()
The match method can also be used to match multiple lines at the same time. This is illustrated in the following example, showing how to match orbit bumps in the two beams of a collider to obtain a given crossing angle between the two beams. Some of the used dipole magnets are shared between the two beams.
import xtrack as xt
# Load a line and build a tracker
collider = xt.Multiline.from_json(
'../../test_data/hllhc15_thick/hllhc15_collider_thick.json')
collider.build_trackers()
tw0 = collider.twiss(method='4d')
opt = collider.match(
lines=['lhcb1', 'lhcb2'],
start=['e.ds.l5.b1', 'e.ds.l5.b2'],
end=['s.ds.r5.b1', 's.ds.r5.b2'],
init=tw0,
vary=xt.VaryList([
'acbxv1.r5', 'acbxv1.l5', # <-- common elements
'acbyvs4.l5b1', 'acbrdv4.r5b1', 'acbcv5.l5b1', # <-- b1
'acbyvs4.l5b2', 'acbrdv4.r5b2', 'acbcv5.r5b2', # <-- b2
],
step=1e-10, limits=[-1e-3, 1e-3]),
targets = [
xt.TargetSet(y=0, py=10e-6, at='ip5', line='lhcb1'),
xt.TargetSet(y=0, py=-10e-6, at='ip5', line='lhcb2'),
xt.TargetSet(y=0, py=0, at=xt.END, line='lhcb1'),
xt.TargetSet(y=0, py=0, at=xt.END, line='lhcb2')
])
opt.target_status()
# prints:
#
# Target status:
# id state tag tol_met residue current_val target_val description
# 0 ON True -3.93023e-19 -3.93023e-19 0 line=lhcb1, ('y', 'ip5'), val=0, tol=1e- ...
# 1 ON True -7.06934e-18 1e-05 1e-05 line=lhcb1, ('py', 'ip5'), val=1e-05, to ...
# 2 ON True -1.76183e-19 -1.76183e-19 0 line=lhcb2, ('y', 'ip5'), val=0, tol=1e- ...
# 3 ON True -1.07353e-17 -1e-05 -1e-05 line=lhcb2, ('py', 'ip5'), val=-1e-05, t ...
# 4 ON True 4.39323e-18 4.39323e-18 0 line=lhcb1, ('y', 's.ds.r5.b1'), val=0, ...
# 5 ON True 2.00777e-19 2.00777e-19 0 line=lhcb1, ('py', 's.ds.r5.b1'), val=0, ...
# 6 ON True 5.23202e-19 5.23202e-19 0 line=lhcb2, ('y', 's.ds.r5.b2'), val=0, ...
# 7 ON True -4.05091e-20 -4.05091e-20 0 line=lhcb2, ('py', 's.ds.r5.b2'), val=0, ...
# Complete source: xtrack/examples/match/004_match_bump_common_elements.py
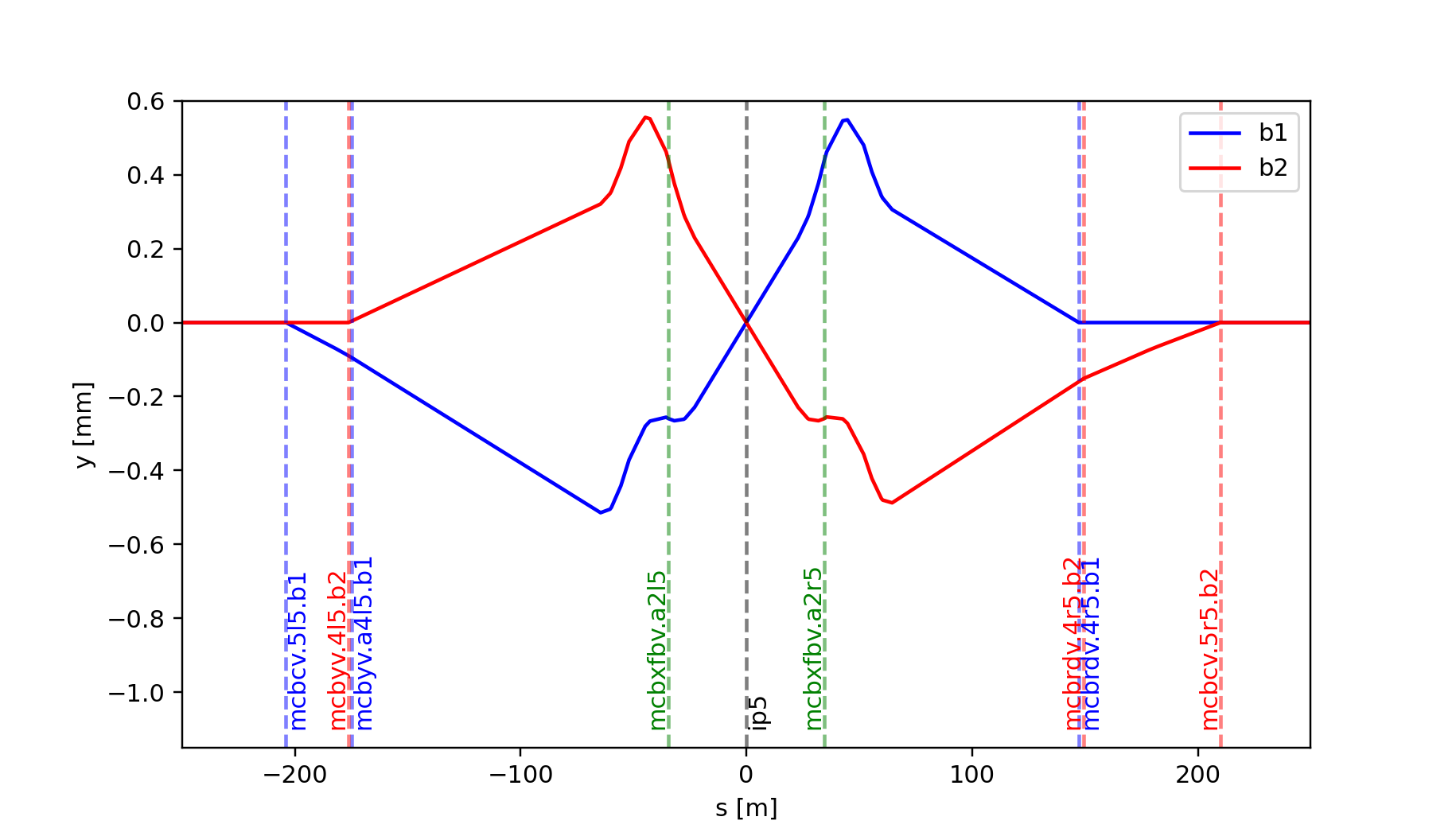
The orbit bump from the example above. The corrector magnets indicated in green act on both beams.
Callables and inequalities in targets
See also xtrack.Line.match()
Targets can contain also callables and inequalities. This is illustrated in the following example, showing the match of crossing bump (as in the previous section) where we use a callable to match the average angle at the IP to zero and inequalities to impose a minimum and maximum value for the angle of one beam at the IP.
import xtrack as xt
# Load a line and build a tracker
collider = xt.Multiline.from_json(
'../../test_data/hllhc15_thick/hllhc15_collider_thick.json')
collider.build_trackers()
tw0 = collider.twiss(method='4d')
opt = collider.match(
lines=['lhcb1', 'lhcb2'],
start=['e.ds.l5.b1', 'e.ds.l5.b2'],
end=['s.ds.r5.b1', 's.ds.r5.b2'],
init=tw0,
vary=xt.VaryList([
'acbxv1.r5', 'acbxv1.l5', # <-- common elements
'acbyvs4.l5b1', 'acbrdv4.r5b1', 'acbcv5.l5b1', # <-- b1
'acbyvs4.l5b2', 'acbrdv4.r5b2', 'acbcv5.r5b2', # <-- b2
],
step=1e-10, limits=[-1e-3, 1e-3]),
targets = [
xt.Target(y=0, at='ip5', line='lhcb1'),
xt.Target('py', xt.GreaterThan(9e-6), at='ip5', line='lhcb1'), # <-- inequality
xt.Target('py', xt.LessThan( 11e-6), at='ip5', line='lhcb1'), # <-- inequality
xt.Target(y=0, at='ip5', line='lhcb2'),
xt.Target(
lambda tw: tw.lhcb1['py', 'ip5'] + tw.lhcb2['py', 'ip5'], value=0), # <-- callable
xt.TargetSet(y=0, py=0, at=xt.END, line='lhcb1'),
xt.TargetSet(y=0, py=0, at=xt.END, line='lhcb2')
])
opt.target_status()
# prints:
#
# Target status:
# id state tag tol_met residue current_val target_val description
# 0 ON True -5.42101e-20 -5.42101e-20 0 line=lhcb1, ('y', 'ip5'), val=0, tol=1e- ...
# 1 ON True -1.99849e-17 9e-06 GreaterThan(9e-06) line=lhcb1, ('py', 'ip5'), val=GreaterTh ...
# 2 ON True 0 9e-06 LessThan(1.1e-05) line=lhcb1, ('py', 'ip5'), val=LessThan( ...
# 3 ON True -4.67562e-19 -4.67562e-19 0 line=lhcb2, ('y', 'ip5'), val=0, tol=1e- ...
# 4 ON True 1.03338e-19 1.03338e-19 0 callable, val=0, tol=1e-10, weight=1
# 5 ON True 3.64674e-18 3.64674e-18 0 line=lhcb1, ('y', 's.ds.r5.b1'), val=0, ...
# 6 ON True 1.68179e-19 1.68179e-19 0 line=lhcb1, ('py', 's.ds.r5.b1'), val=0, ...
# 7 ON True 2.05694e-18 2.05694e-18 0 line=lhcb2, ('y', 's.ds.r5.b2'), val=0, ...
# 8 ON True -1.21224e-19 -1.21224e-19 0 line=lhcb2, ('py', 's.ds.r5.b2'), val=0, ...
# Complete source: xtrack/examples/match/005_match_bump_common_ele_callable_ineq.py
Matching on results of arbitrary actions
See also xtrack.Line.match()
By default the quantities used as match targets are found in the result of the
twiss method. It is nevertheless possible to use the match method on results of
arbitrary user-defined “actions”. Each action is defined by writing a small python
class inheriting from xtrack.Action providing a method called run,
called at each optimization step, which returns a dictionary of quantities that
can be used as targets. This is illustrated by the following example, showing
how to use octupole magnets to control the detuning with amplitude coefficients
(det_xx = dqx/dJx and det_yy = dqy/dJy) as obtained by tracking.
import xtrack as xt
# Load a line and build a tracker
line = xt.Line.from_json('../../test_data/hllhc15_thick/lhc_thick_with_knobs.json')
line.build_tracker()
class ActionMeasAmplDet(xt.Action):
def __init__(self, line, num_turns, nemitt_x, nemitt_y):
self.line = line
self.num_turns = num_turns
self.nemitt_x = nemitt_x
self.nemitt_y = nemitt_y
def run(self):
det_coefficients = self.line.get_amplitude_detuning_coefficients(
nemitt_x=self.nemitt_x, nemitt_y=self.nemitt_y,
num_turns=self.num_turns)
out = {'d_xx': det_coefficients['det_xx'],
'd_yy': det_coefficients['det_yy']}
return out
action = ActionMeasAmplDet(line=line, nemitt_x=2.5e-6, nemitt_y=2.5e-6,
num_turns=128)
opt = line.match(vary=xt.VaryList(['kof.a23b1', 'kod.a23b1'], step=1.),
targets=[action.target('d_xx', 1000., tol=0.1),
action.target('d_yy', 2000., tol=0.1)])
opt.target_status()
# prints:
#
# Target status:
# id state tag tol_met residue current_val target_val description
# 0 ON True 0.0844456 1000.08 1000 'd_xx', val=1000, ...
# 1 ON True -0.00209987 2000 2000 'd_yy', val=2000, ...
# Complete source: xtrack/examples/match/006_match_action.py
Interactive match
See also xtrack.Line.match()
The match method can also be used in an interactive way passing solve=False
to the xtrack.Line.match(). In this case an xdeps.Optimize object
is returned that can be used to interactively drive the optimization process,
by enabling/disabling knobs and targets, changing target values and tolerances,
controlling the number of optimization steps, tagging and reloading specific
optimization steps. This is illustrated in the following example.
import xtrack as xt
# Load a line and build a tracker
line = xt.Line.from_json('../../test_data/hllhc15_thick/lhc_thick_with_knobs.json')
line.build_tracker()
# Build optimizer object for tunes and chromaticities without performing optimization
opt = line.match(
solve=False, # <--
method='4d',
vary=[
xt.VaryList(['kqtf.b1', 'kqtd.b1'], step=1e-8, tag='quad'),
xt.VaryList(['ksf.b1', 'ksd.b1'], step=1e-4, limits=[-0.1, 0.1], tag='sext'),
],
targets = [
xt.TargetSet(qx=62.315, qy=60.325, tol=1e-6, tag='tune'),
xt.TargetSet(dqx=10.0, dqy=12.0, tol=0.01, tag='chrom'),
])
opt.target_status()
# prints the following (optimization not performed):
#
# Target status:
# id state tag tol_met residue current_val target_val description
# 0 ON tune False -0.00499997 62.31 62.315 'qx', val=62.315, tol=1e-06, weight=10)
# 1 ON tune False -0.005 60.32 60.325 'qy', val=60.325, tol=1e-06, weight=10)
# 2 ON chrom False -8.09005 1.90995 10 'dqx', val=10, tol=0.01, weight=1)
# 3 ON chrom False -10.057 1.94297 12 'dqy', val=12, tol=0.01, weight=1)
# Disable optimization of chromaticities and usage of sextupole knobs
opt.disable_targets(tag='chrom')
opt.disable_vary(tag='sext')
opt.show()
# prints:
#
# Vary:
# id tag state description
# 0 quad ON name='kqtf.b1', limits=None, step=1e-08, weight=1)
# 1 quad ON name='kqtd.b1', limits=None, step=1e-08, weight=1)
# 2 sext OFF name='ksf.b1', limits=(-0.1, 0.1), step=0.0001, weight=1)
# 3 sext OFF name='ksd.b1', limits=(-0.1, 0.1), step=0.0001, weight=1)
# Targets:
# id tag state description
# 0 tune ON 'qx', val=62.315, tol=1e-06, weight=10)
# 1 tune ON 'qy', val=60.325, tol=1e-06, weight=10)
# 2 chrom OFF 'dqx', val=10, tol=0.01, weight=1)
# 3 chrom OFF 'dqy', val=12, tol=0.01, weight=1)
# Solve (for tunes only)
opt.solve()
opt.target_status()
# prints:
# Target status:
# id state tag tol_met residue current_val target_val description
# 0 ON tune True -4.51905e-12 62.315 62.315 'qx', val=62.315, tol=1e-06, weight=10)
# 1 ON tune True 9.23706e-14 60.325 60.325 'qy', val=60.325, tol=1e-06, weight=10)
# 2 OFF chrom False 0 1.89374 10 'dqx', val=10, tol=0.01, weight=1)
# 3 OFF chrom False 0 1.91882 12 'dqy', val=12, tol=0.01, weight=1)
# Enable all targets and knobs
opt.enable_all_targets()
opt.enable_all_vary()
# Solve (for tunes and chromaticities)
opt.solve()
opt.target_status()
# prints:
# Target status:
# id state tag tol_met residue current_val target_val description
# 0 ON tune True -5.62885e-10 62.315 62.315 'qx', val=62.315, tol=1e-06, weight=10)
# 1 ON tune True 2.67875e-11 60.325 60.325 'qy', val=60.325, tol=1e-06, weight=10)
# 2 ON chrom True -0.000156234 9.99984 10 'dqx', val=10, tol=0.01, weight=1)
# 3 ON chrom True -9.81714e-07 12 12 'dqy', val=12, tol=0.01, weight=1)
# Change a target value and the corresponding tolerance
opt.targets[1].value = 60.05
opt.targets[1].tol = 1e-10
opt.target_status()
# prints:
# Target status:
# id state tag tol_met residue current_val target_val description
# 0 ON tune True -5.62885e-10 62.315 62.315 'qx', val=62.315, tol=1e-06, weight=10)
# 1 ON tune False 0.275 60.325 60.05 'qy', val=60.05, tol=1e-10, weight=10)
# 2 ON chrom True -0.000156234 9.99984 10 'dqx', val=10, tol=0.01, weight=1)
# 3 ON chrom True -9.81714e-07 12 12 'dqy', val=12, tol=0.01, weight=1)
# Perform two optimization steps (without checking for convergence)
opt.step(2)
opt.target_status()
# prints (two steps were not enough to reach convergence):
# Target status:
# id state tag tol_met residue current_val target_val description
# 0 ON tune True 4.55631e-08 62.315 62.315 'qx', val=62.315, tol=1e-06, weight=10)
# 1 ON tune False 2.56767e-09 60.05 60.05 'qy', val=60.05, tol=1e-10, weight=10)
# 2 ON chrom True -0.000127644 9.99987 10 'dqx', val=10, tol=0.01, weight=1)
# 3 ON chrom True -2.44325e-05 12 12 'dqy', val=12, tol=0.01, weight=1)
# Perform additional two steps
opt.step(2)
opt.target_status()
# prints (convergence was reached):
#
# Target status:
# id state tag tol_met residue current_val target_val description
# 0 ON tune True -4.00533e-11 62.315 62.315 'qx', val=62.315, tol=1e-06, weight=10)
# 1 ON tune True 1.42109e-14 60.05 60.05 'qy', val=60.05, tol=1e-10, weight=10)
# 2 ON chrom True 3.19579e-07 10 10 'dqx', val=10, tol=0.01, weight=1)
# 3 ON chrom True -1.30694e-09 12 12 'dqy', val=12, tol=0.01, weight=1)
# Tag present configuration
opt.tag(tag='my_tag')
# Reload initial configuration
opt.reload(iteration=0)
opt.target_status()
# prints:
#
# Target status:
# id state tag tol_met residue current_val target_val description
# 0 ON tune False -0.00499997 62.31 62.315 'qx', val=62.315, tol=1e-06, weight=10
# 1 ON tune False 0.27 60.32 60.05 'qy', val=60.05, tol=1e-10, weight=10
# 2 ON chrom False -8.09005 1.90995 10 'dqx', val=10, tol=0.01, weight=1
# 3 ON chrom False -10.057 1.94297 12 'dqy', val=12, tol=0.01, weight=1
# Reload tagged configuration
opt.reload(tag='my_tag')
opt.target_status()
# Target status:
# id state tag tol_met residue current_val target_val description
# 0 ON tune True -4.00533e-11 62.315 62.315 'qx', val=62.315, tol=1e-06, weight=10
# 1 ON tune True 1.42109e-14 60.05 60.05 'qy', val=60.05, tol=1e-10, weight=10
# 2 ON chrom True 3.19579e-07 10 10 'dqx', val=10, tol=0.01, weight=1
# 3 ON chrom True -1.30694e-09 12 12 'dqy', val=12, tol=0.01, weight=1
# Complete source: xtrack/examples/match/001_match_interactive.py
Create new knobs by matching
See also xtrack.Line.match_knob()
The xtrack.Line.match_knob() method allows generating new knobs based on
the result of an optimization. The user can specify a value for
knob_value_start corresponding to the line state before the optimization,
and a value for knob_value_end corresponding to the line state after the
optimization. A linear interpolation is used when a different value of the knob
is set. This shown by the following example, which shows how to build knobs
controlling the horizontal and vertical chromaticities of a line.
import xtrack as xt
# Load a line and build a tracker
line = xt.Line.from_json('../../test_data/hllhc15_thick/lhc_thick_with_knobs.json')
line.build_tracker()
tw0 = line.twiss(method='4d')
# Knob optimizer for horizontal chromaticity
opt = line.match_knob('dqx.b1', knob_value_start=tw0.dqx, knob_value_end=3.0,
run=False, method='4d',
vary=xt.VaryList(['ksf.b1', 'ksd.b1'], step=1e-8),
targets=xt.TargetSet(dqx=3.0, dqy=tw0, tol=1e-6))
# New terms have been added to knobs to vary
line.vars['ksf.b1']._expr # is: (0.0 + vars['ksf.b1_from_dqx.b1'])
line.vars['ksd.b1']._expr # is: (0.0 + vars['ksd.b1_from_dqx.b1'])
line.vars['ksf.b1_from_dqx.b1']._expr # is None
line.vars['ksd.b1_from_dqx.b1']._expr # is None
# optimized acts on newly created terms
opt.vary_status(); opt.target_status()
# prints:
#
# Vary status:
# id state tag name lower_limit current_val upper_limit val_at_iter_0 step weight
# 0 ON ksf.b1_from_dqx.b1 None 0 None 0 1e-08 1
# 1 ON ksd.b1_from_dqx.b1 None 0 None 0 1e-08 1
# Target status:
# id state tag tol_met residue current_val target_val description
# 0 ON False -1.09005 1.90995 3 'dqx', val=3, tol=1e-06, weight=1
# 1 ON True 0 1.94297 1.94297 'dqy', val=1.94297, tol=1e-06, weight=1
opt.solve() # perform optimization
opt.vary_status(); opt.target_status()
# prints:
#
# Vary status:
# id state tag name lower_limit current_val upper_limit val_at_iter_0 step weight
# 0 ON ksf.b1_from_dqx.b1 None 0.00130336 None 0 1e-08 1
# 1 ON ksd.b1_from_dqx.b1 None -0.0004024 None 0 1e-08 1
# Target status:
# id state tag tol_met residue current_val target_val description
# 0 ON True 7.94672e-08 3 3 'dqx', val=3, tol=1e-06, weight=1
# 1 ON True 0 1.94297 1.94297 'dqy', val=1.94297, tol=1e-06, weight=1
# Generate the knob
opt.generate_knob()
line.vars['ksf.b1']._expr # is: (0.0 + vars['ksf.b1_from_dqx.b1'])
line.vars['ksd.b1']._expr # is: (0.0 + vars['ksd.b1_from_dqx.b1'])
line.vars['ksf.b1_from_dqx.b1']._expr
# is ((0.0011956933485755728 * vars['dqx.b1']) - 0.0022837181704350494)
line.vars['ksd.b1_from_dqx.b1']._expr # is None
# is ((-0.0003691583859286993 * vars['dqx.b1']) - -0.0007050751889840094)
# Create also vertical chromaticity knob
opt_dqy = line.match_knob('dqy.b1', knob_value_start=tw0.dqy, knob_value_end=3.0,
run=False, method='4d',
vary=xt.VaryList(['ksf.b1', 'ksd.b1'], step=1e-8),
targets=xt.TargetSet(dqx=tw0, dqy=3.0, tol=1e-6))
opt_dqy.solve()
opt_dqy.generate_knob()
line.vars['ksf.b1']._expr
# is: ((0.0 + vars['ksf.b1_from_dqx.b1']) + vars['ksf.b1_from_dqy.b1'])
line.vars['ksd.b1']._expr
# is: ((0.0 + vars['ksd.b1_from_dqx.b1']) + vars['ksd.b1_from_dqy.b1'])
line.vars['ksf.b1_from_dqx.b1']._expr
# is ((0.0011956933485755728 * vars['dqx.b1']) - 0.0022837181704350494)
line.vars['ksd.b1_from_dqx.b1']._expr # is None
# is ((-0.0003691583859286993 * vars['dqx.b1']) - -0.0007050751889840094)
line.vars['ksf.b1_from_dqy.b1']._expr
# is ((0.0011956933485755728 * vars['dqy.b1']) - 0.0022837181704350494)
line.vars['ksd.b1_from_dqy.b1']._expr
# is ((-0.0003691583859286993 * vars['dqy.b1']) - -0.0007050751889840094)
# Test knobs
line.vars['dqx.b1'] = 5.
line.vars['dqy.b1'] = 6.
tw = line.twiss(method='4d')
tw.dqx # is 5.00000231
tw.dqy # is 5.99999987
# Complete source: xtrack/examples/match/007_match_knob.py