Twiss
Xtrack provides a twiss method associated to the line that can be used to
obtain the lattice functions and other quantities like tunes, chromaticities,
slip factor, etc. This is illustrated in the following examples. For a complete
description of all available options and output quantities, please refer to the
xtrack.Line.twiss() method documentation.
Basic usage (ring)
The following example shows how to use the twiss method to obtain the lattice functions and other quantities for a ring.
import numpy as np
import xtrack as xt
# Load a line and build tracker
line = xt.Line.from_json(
'../../test_data/hllhc15_thick/lhc_thick_with_knobs.json')
line.particle_ref = xt.Particles(mass0=xt.PROTON_MASS_EV, q0=1, energy0=7e12)
line.vars['vrf400'] = 16
line.build_tracker()
# Twiss
tw = line.twiss()
# Inspect tunes and chromaticities
tw.qx # Horizontal tune
tw.qy # Vertical tune
tw.dqx # Horizontal chromaticity
tw.dqy # Vertical chromaticity
# Plot closed orbit and lattice functions
import matplotlib.pyplot as plt
plt.close('all')
fig1 = plt.figure(1, figsize=(6.4, 4.8*1.5))
spbet = plt.subplot(3,1,1)
spco = plt.subplot(3,1,2, sharex=spbet)
spdisp = plt.subplot(3,1,3, sharex=spbet)
spbet.plot(tw.s, tw.betx)
spbet.plot(tw.s, tw.bety)
spbet.set_ylabel(r'$\beta_{x,y}$ [m]')
spco.plot(tw.s, tw.x)
spco.plot(tw.s, tw.y)
spco.set_ylabel(r'(Closed orbit)$_{x,y}$ [m]')
spdisp.plot(tw.s, tw.dx)
spdisp.plot(tw.s, tw.dy)
spdisp.set_ylabel(r'$D_{x,y}$ [m]')
spdisp.set_xlabel('s [m]')
fig1.suptitle(
r'$q_x$ = ' f'{tw.qx:.5f}' r' $q_y$ = ' f'{tw.qy:.5f}' '\n'
r"$Q'_x$ = " f'{tw.dqx:.2f}' r" $Q'_y$ = " f'{tw.dqy:.2f}'
r' $\gamma_{tr}$ = ' f'{1/np.sqrt(tw.momentum_compaction_factor):.2f}'
)
fig1.subplots_adjust(left=.15, right=.92, hspace=.27)
plt.show()
# Complete source: xtrack/examples/twiss/000_twiss.py
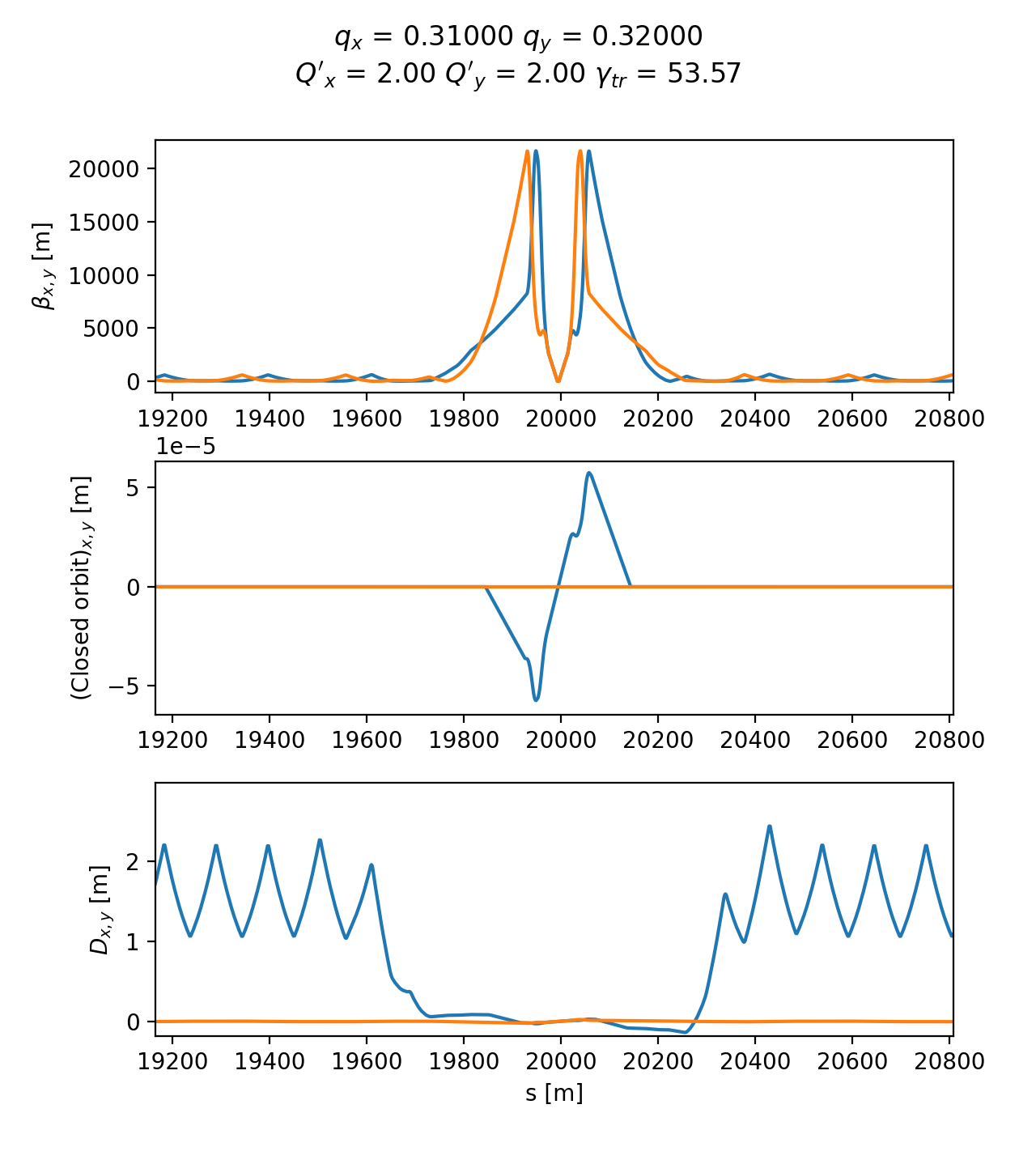
Lattice functions and accelerator parameters as obtained by Xtrack twiss.
Inspecting twiss output
The twiss table has several access options as illustrated in the following example.
import numpy as np
import xtrack as xt
# Load a line and build tracker
line = xt.Line.from_json(
'../../test_data/hllhc15_thick/lhc_thick_with_knobs.json')
line.particle_ref = xt.Particles(
mass0=xt.PROTON_MASS_EV, q0=1, energy0=7e12)
line.build_tracker()
# Twiss
tw = line.twiss(method='4d')
# Print table
tw.show()
# prints:
#
# name s x px y py zeta delta ptau betx bety alfx ...
# ip7 0 0 0 0 0 0 0 0 120.813 149.431
# drift_0 0 0 0 0 0 0 0 0 120.813 149.431
# tcsg.a4r7.b1_entry 0.5 0 0 0 0 0 0 0 119.542 150.821
# tcsg.a4r7.b1 0.5 0 0 0 0 0 0 0 119.542 150.821
# tcsg.a4r7.b1_exit 1.5 0 0 0 0 0 0 0 117.031 153.63
# drift_1 1.5 0 0 0 0 0 0 0 117.031 153.63
# ...
# tcsg.a4l7.b1 26655.4 0 0 0 0 0 0 0 130.019 139.974
# tcsg.a4l7.b1_exit 26656.4 0 0 0 0 0 0 0 127.334 142.627
# drift_6661 26656.4 0 0 0 0 0 0 0 127.334 142.627
# lhcb1ip7_p_ 26658.9 0 0 0 0 0 0 0 120.813 149.431
# _end_point 26658.9 0 0 0 0 0 0 0 120.813 149.431
# Access to scalar quantities
tw.qx # is : 62.31000
tw['qx'] # is : 62.31000
# Access to a single column of the table
tw['betx'] # is an array with the horizontal beta function at all elements
# Access to a single element of the table of a vector quantity
tw['betx', 'ip1'] # is 0.150000
# Regular expressions can be used to select elements by name
tw.rows['ip.*']
# returns:
#
# TwissTable: 9 rows, 41 cols
# name s x px y py zeta delta ptau betx bety ...
# ip7 0 0 0 0 0 0 0 0 120.813 149.431
# ip8 3321.22 0 0 0 0 0 0 0 1.5 1.5
# ip1.l1 6664.72 0 0 0 0 0 0 0 0.15 0.15
# ip1 6664.72 0 0 0 0 0 0 0 0.15 0.15
# ip2 9997.16 0 0 0 0 0 0 0 10 10
# ip3 13329.4 0 0 0 0 0 0 0 121.567 218.584
# ip4 16661.7 0 0 0 0 0 0 0 236.18 306.197
# ip5 19994 0 0 0 0 0 0 0 0.15 0.15
# ip6 23326.4 0 0 0 0 0 0 0 273.434 183.74
# A section of the ring can be selected using names
tw.rows['ip5':'mqxfa.a1r5_exit']
# returns:
#
# TwissTable: 16 rows, 41 cols
# name s x px y py zeta delta ptau betx bety ...
# ip5 19994 0 0 0 0 0 0 0 0.15 0.15
# mbcs2.1r5_entry 19994 0 0 0 0 0 0 0 0.15 0.15
# mbcs2.1r5 19994 0 0 0 0 0 0 0 0.15 0.15
# mbcs2.1r5_exit 20000.5 0 0 0 0 0 0 0 281.817 281.817
# drift_5020 20000.5 0 0 0 0 0 0 0 281.817 281.817
# taxs.1r5_entry 20013.1 0 0 0 0 0 0 0 2419.5 2419.5
# taxs.1r5 20013.1 0 0 0 0 0 0 0 2419.5 2419.5
# taxs.1r5_exit 20014.9 0 0 0 0 0 0 0 2898.3 2898.3
# drift_5021 20014.9 0 0 0 0 0 0 0 2898.3 2898.3
# bpmqstza.1r5.b1_entry 20015.9 0 0 0 0 0 0 0 3189.09 3189.09
# bpmqstza.1r5.b1 20015.9 0 0 0 0 0 0 0 3189.09 3189.09
# bpmqstza.1r5.b1_exit 20015.9 0 0 0 0 0 0 0 3189.09 3189.09
# drift_5022 20015.9 0 0 0 0 0 0 0 3189.09 3189.09
# mqxfa.a1r5_entry 20016.9 0 0 0 0 0 0 0 3504.46 3504.47
# mqxfa.a1r5 20016.9 0 0 0 0 0 0 0 3504.46 3504.47
# mqxfa.a1r5_exit 20021.1 0 0 0 0 0 0 0 4478.55 5360.39
# A section of the ring can be selected using the s coordinate
tw.rows[300:305:'s']
# returns:
#
# TwissTable: 10 rows, 41 cols
# name s x px y py zeta delta ptau betx bety ...
# bpm.8r7.b1_entry 300.698 0 0 0 0 0 0 0 22.6944 174
# bpm.8r7.b1 300.698 0 0 0 0 0 0 0 22.6944 174
# bpm.8r7.b1_exit 300.698 0 0 0 0 0 0 0 22.6944 174
# drift_52 300.698 0 0 0 0 0 0 0 22.6944 174
# mq.8r7.b1_entry 301.695 0 0 0 0 0 0 0 21.8586 178.331
# mq.8r7.b1 301.695 0 0 0 0 0 0 0 21.8586 178.331
# mq.8r7.b1_exit 304.795 0 0 0 0 0 0 0 21.6904 176.923
# drift_53 304.795 0 0 0 0 0 0 0 21.6904 176.923
# mqtli.8r7.b1_entry 304.964 0 0 0 0 0 0 0 21.8057 176.036
# mqtli.8r7.b1 304.964 0 0 0 0 0 0 0 21.8057 176.036
# A section of the ring can be selected using indexes relative one element
# (e.g. to get from three elements upstream of 'ip1' to two elements
# downstream of 'ip1')
tw.rows['ip5%%-3':'ip5%%2']
# returns:
#
# TwissTable: 6 rows, 41 cols
# name s x px y py zeta delta ptau betx bety ...
# mbcs2.1l5_entry 19987.5 0 0 0 0 0 0 0 281.817 281.817
# mbcs2.1l5 19987.5 0 0 0 0 0 0 0 281.817 281.817
# mbcs2.1l5_exit 19994 0 0 0 0 0 0 0 0.15 0.15
# ip5 19994 0 0 0 0 0 0 0 0.15 0.15
# mbcs2.1r5_entry 19994 0 0 0 0 0 0 0 0.15 0.15
# mbcs2.1r5 19994 0 0 0 0 0 0 0 0.15 0.15
# Columns can be selected as well (and defined on the fly with simple mathematical
# expressions)
tw.cols['betx dx/sqrt(betx)']
# returns:
#
# TwissTable: 30699 rows, 3 cols
# TwissTable: 10 rows, 3 cols
# name betx dx/sqrt(betx)
# ip7 120.813 -0.0185459
# drift_0 120.813 -0.0185459
# tcsg.a4r7.b1_entry 119.542 -0.0186442
# tcsg.a4r7.b1 119.542 -0.0186442
# tcsg.a4r7.b1_exit 117.031 -0.0188431
# ...
# Each of the selection methods above returns a valid table, hence selections
# can be chained. For example we can get the beta functions at all the skew
# quadrupoles between ip1 and ip2:
tw.rows['ip1':'ip2'].rows['mqs.*b1'].cols['betx bety']
# returns:
#
# TwissTable: 4 rows, 3 cols
# name betx bety
# mqs.23r1.b1 574.134 57.4386
# mqs.27r1.b1 574.134 57.4386
# mqs.27l2.b1 59.8967 62.0111
# mqs.23l2.b1 59.8968 62.011
# Complete source: xtrack/examples/twiss/017_table_slicing.py
4d method (RF off)
When the RF cavities are disabled or not included in the lattice (or when the longitudinal motion is artificially frozen) it is not possible to use the standard method for the twiss calculation. In these cases, the “4d” method can be used, as illustrated in the following examples:
import xtrack as xt
# Load a line and build tracker
line = xt.Line.from_json(
'../../test_data/hllhc15_noerrors_nobb/line_and_particle.json')
line.particle_ref = xt.Particles(mass0=xt.PROTON_MASS_EV, q0=1, energy0=7e12)
line.build_tracker()
# We consider a case in which all RF cavities are off
tab = line.get_table()
tab_cav = tab.rows[tab.element_type == 'Cavity']
for nn in tab_cav.name:
line[nn].voltage = 0
# For this configuration, `line.twiss()` gives an error because the
# longitudinal motion is not stable.
# In this case, the '4d' method of `line.twiss()` can be used to compute the
# twiss parameters.
tw = line.twiss(method='4d')
# Complete source: xtrack/examples/twiss/008_4d_twiss_and_particle_match.py
Off-momentum twiss
The 4d mode of the twiss can be used providing in input the initial momentum. This feature can be used to measure the non-linear momentum detuning of a ring as shown in the following example:
import numpy as np
from cpymad.madx import Madx
import xtrack as xt
mad = Madx()
mad.call('../../test_data/hllhc15_noerrors_nobb/sequence.madx')
mad.use('lhcb1')
line = xt.Line.from_madx_sequence(mad.sequence.lhcb1)
line.particle_ref = xt.Particles(p0c=7000e9, mass0=xt.PROTON_MASS_EV)
line.build_tracker()
tw = line.twiss()
delta_values = np.linspace(-5e-3, 5e-3, 100)
qx_values = delta_values * 0
qy_values = delta_values * 0
for i, delta in enumerate(delta_values):
print(f'Xsuite working on {i} of {len(delta_values)} ', end='\r', flush=True)
tt = line.twiss(method='4d', delta0=delta)
qx_values[i] = tt.qx
qy_values[i] = tt.qy
# Complete source: xtrack/examples/twiss/011_tune_vs_delta.py

Twiss with “initial” conditions
The twiss calculation can be performed with initial conditions provided by the users or extracted from an existing twiss table, as illustrated in the following example:
import xtrack as xt
# Load a line and build tracker
line = xt.Line.from_json(
'../../test_data/hllhc15_noerrors_nobb/line_and_particle.json')
line.particle_ref = xt.Particles(mass0=xt.PROTON_MASS_EV, q0=1, energy0=7e12)
line.build_tracker()
# Periodic twiss
tw_p = line.twiss()
# Twiss over a range with user-defined initial conditions (at start)
tw1 = line.twiss(start='ip5', end='mb.c24r5.b1',
betx=0.15, bety=0.15, py=1e-6)
# Twiss over a range with user-defined initial conditions at end
tw2 = line.twiss(start='ip5', end='mb.c24r5.b1', init_at=xt.END,
alfx=3.50482, betx=131.189, alfy=-0.677173, bety=40.7318,
dx=1.22515, dpx=-0.0169647)
# Twiss over a range with user-defined initial conditions at arbitrary location
tw3 = line.twiss(start='ip5', end='mb.c24r5.b1', init_at='mb.c14r5.b1',
alfx=-0.437695, betx=31.8512, alfy=-6.73282, bety=450.454,
dx=1.22606, dpx=-0.0169647)
# Initial conditions can also be taken from an existing twiss table
tw4 = line.twiss(start='ip5', end='mb.c24r5.b1', init_at='mb.c14r5.b1',
init=tw_p)
# More explicitly, a `TwissInit` object can be extracted from the twiss table
# and used as initial conditions
tw_init = tw_p.get_twiss_init('mb.c14r5.b1',)
tw5 = line.twiss(start='ip5', end='mb.c24r5.b1', init=tw_init)
# Complete source: xtrack/examples/twiss/000a_twiss_range.py
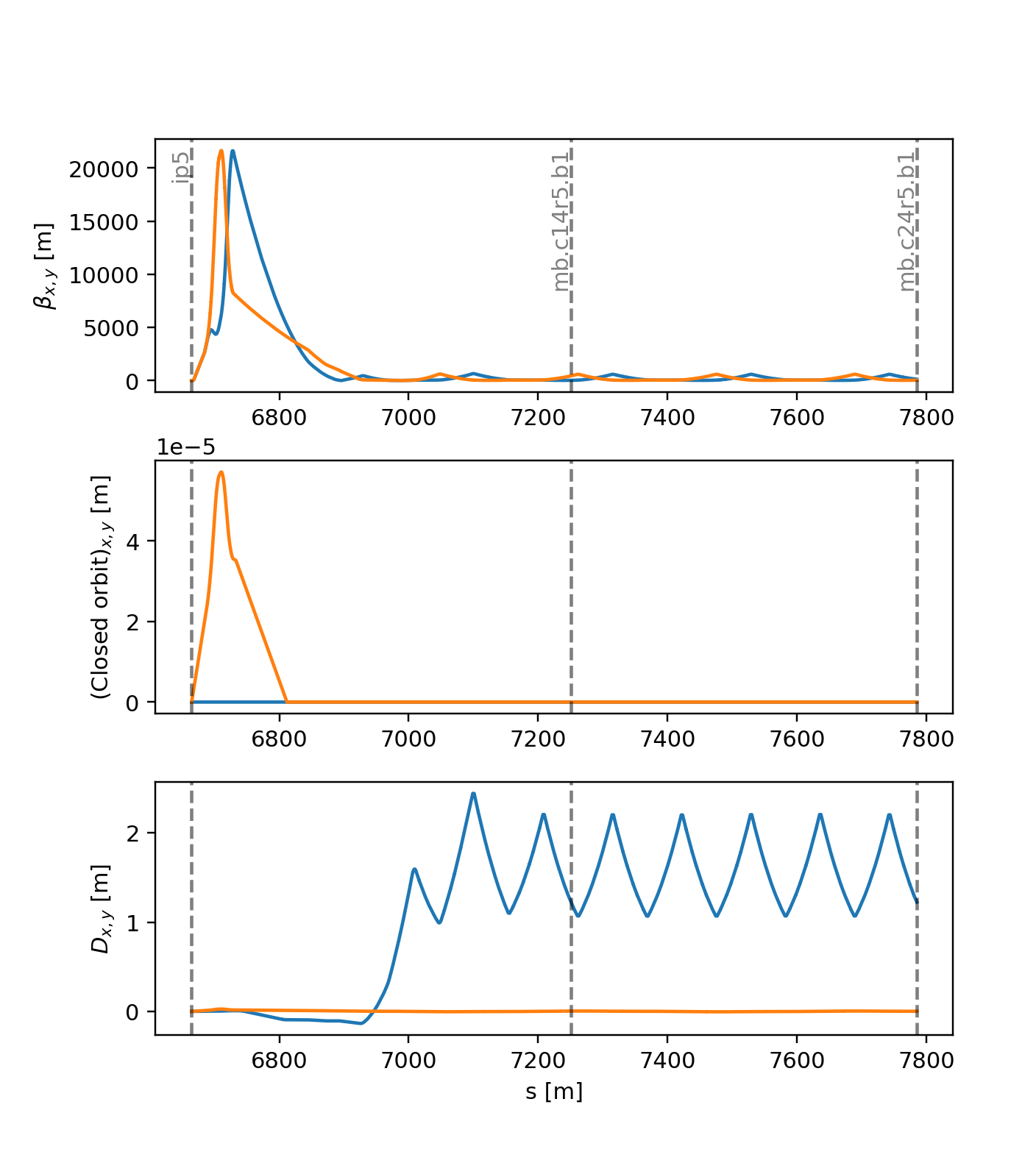
Result of all twiss calculations with initial conditions shown in the example above.
Periodic twiss on a portion of a line
The twiss method can also be used to find the periodic solution for a portion of a beam line, as illustrated in the following example:
import xtrack as xt
# Load a line and build tracker
line = xt.Line.from_json(
'../../test_data/hllhc15_noerrors_nobb/line_and_particle.json')
line.particle_ref = xt.Particles(mass0=xt.PROTON_MASS_EV, q0=1, energy0=7e12)
line.build_tracker()
# Periodic twiss of the full ring
tw_p = line.twiss()
# Periodic twiss of an arc cell
tw = line.twiss(method='4d', start='mq.14r6.b1', end='mq.16r6.b1', init='periodic')
# Complete source: xtrack/examples/twiss/000b_twiss_range_periodic.py
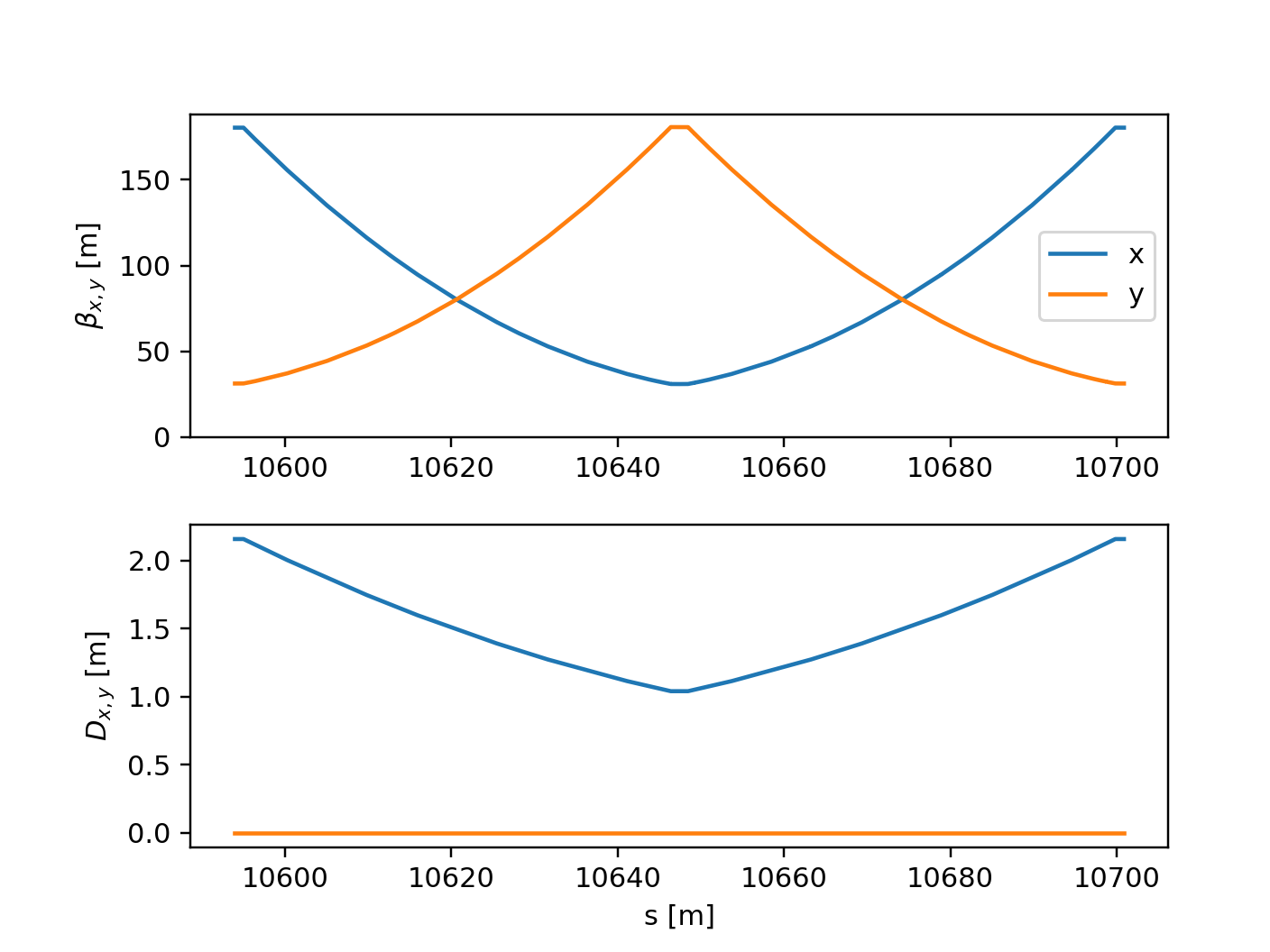
Result of the twiss with periodic boundary conditions.
Beam sizes from twiss table
The transverse and longitudinal beam sizes can be computed from the twiss table, as illustrated in the following example:
import numpy as np
import xtrack as xt
# Load a line and build tracker
line = xt.Line.from_json(
'../../test_data/hllhc15_noerrors_nobb/line_and_particle.json')
line.particle_ref = xt.Particles(mass0=xt.PROTON_MASS_EV, q0=1, energy0=7e12)
line.build_tracker()
# Twiss
tw = line.twiss()
# Transverse normalized emittances
nemitt_x = 2.5e-6
nemitt_y = 2.5e-6
# Longitudinal emittance from energy spread
sigma_pzeta = 2e-4
gemitt_zeta = sigma_pzeta**2 * tw.bets0
# similarly, if the bunch length is known, the emittance can be computed as
# gemitt_zeta = sigma_zeta**2 / tw.bets0
# Compute beam sizes
beam_sizes = tw.get_beam_covariance(nemitt_x=nemitt_x, nemitt_y=nemitt_y,
gemitt_zeta=gemitt_zeta)
# Inspect beam sizes (table can be accessed similarly to twiss tables)
beam_sizes.rows['ip.?'].show()
# prints
#
# name s sigma_x sigma_y sigma_zeta sigma_px ...
# ip3 0 0.000226516 0.000270642 0.19694 4.35287e-06
# ip4 3332.28 0.000281326 0.000320321 0.196941 1.30435e-06
# ip5 6664.57 7.0898e-06 7.08975e-06 0.19694 4.7265e-05
# ip6 9997.01 0.000314392 0.000248136 0.196939 1.61401e-06
# ip7 13329.4 0.000205156 0.000223772 0.196939 2.70123e-06
# ip8 16650.7 2.24199e-05 2.24198e-05 0.196939 1.49465e-05
# ip1 19994.2 7.08975e-06 7.08979e-06 0.196939 4.72651e-05
# ip2 23326.6 5.78877e-05 5.78878e-05 0.196939 5.78879e-06
# All covariances are computed including those from linear coupling
beam_sizes.keys()
# is:
#
# ['s', 'name', 'sigma_x', 'sigma_y', 'sigma_zeta', 'sigma_px', 'sigma_py',
# 'sigma_pzeta', 'Sigma', 'Sigma11', 'Sigma12', 'Sigma13', 'Sigma14', 'Sigma15',
# 'Sigma16', 'Sigma21', 'Sigma22', 'Sigma23', 'Sigma24', 'Sigma25', 'Sigma26',
# 'Sigma31', 'Sigma32', 'Sigma33', 'Sigma34', 'Sigma41', 'Sigma42', 'Sigma43',
# 'Sigma44', 'Sigma51', 'Sigma52'])
# Plot
import matplotlib.pyplot as plt
plt.close('all')
fig1 = plt.figure(1, figsize=(6.4, 4.8*1.5))
spbet = plt.subplot(3,1,1)
spdisp = plt.subplot(3,1,2, sharex=spbet)
spbsz = plt.subplot(3,1,3, sharex=spbet)
spbet.plot(tw.s, tw.betx)
spbet.plot(tw.s, tw.bety)
spbet.set_ylabel(r'$\beta_{x,y}$ [m]')
spdisp.plot(tw.s, tw.dx)
spdisp.plot(tw.s, tw.dy)
spdisp.set_ylabel(r'$D_{x,y}$ [m]')
spbsz.plot(beam_sizes.s, beam_sizes.sigma_x)
spbsz.plot(beam_sizes.s, beam_sizes.sigma_y)
spbsz.set_ylabel(r'$\sigma_{x,y}$ [m]')
spbsz.set_xlabel('s [m]')
spbet.set_xlim(tw['s', 'ip5'] - 2000, tw['s', 'ip5'] + 2000)
fig1.subplots_adjust(left=.15, right=.92, hspace=.27)
plt.show()
# Complete source: xtrack/examples/twiss/018_compute_beam_sizes.py
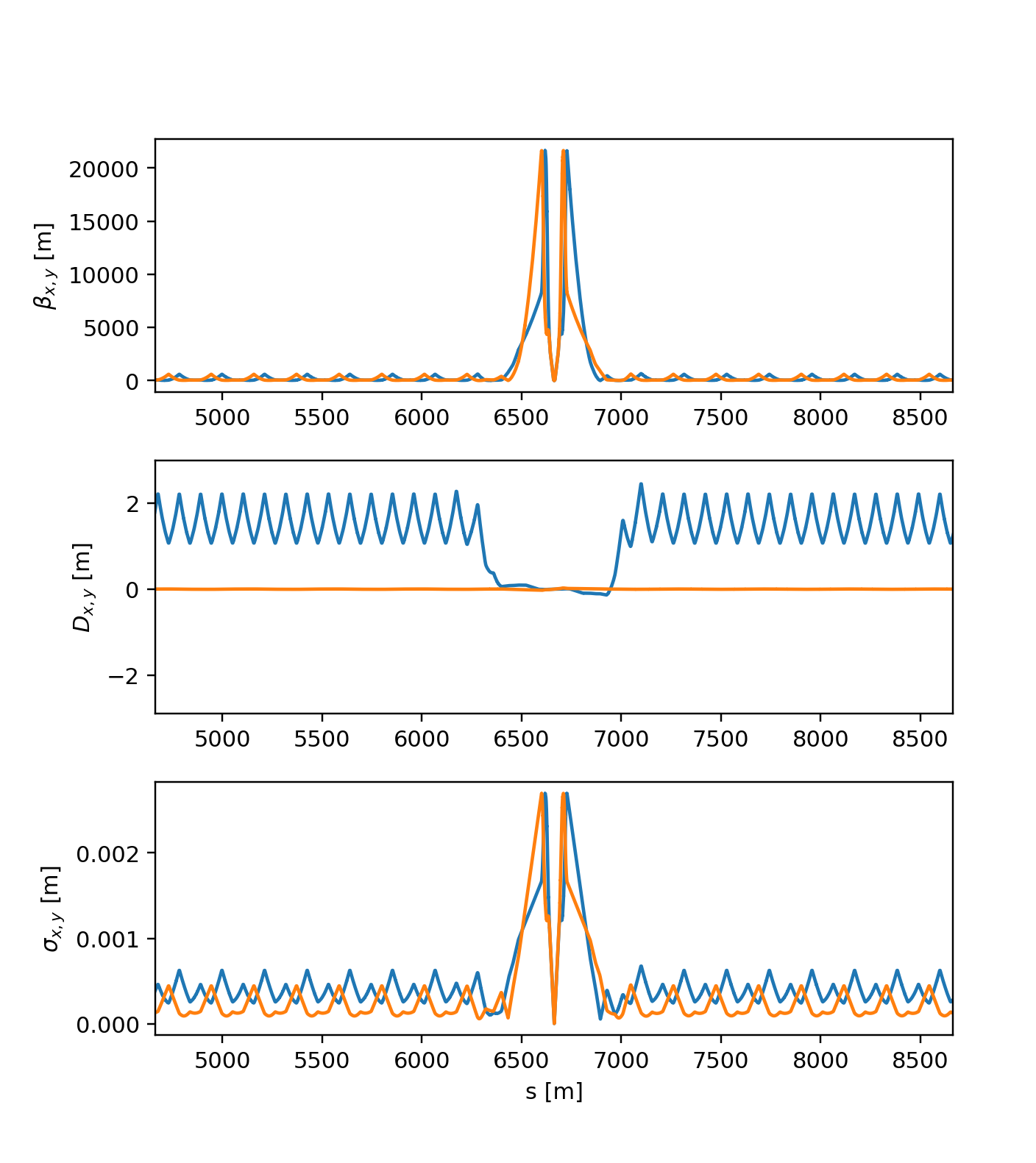
Beam sizes as obtained from twiss.
Particles normalized coordinates
The twiss table holds the information to convert particle physical coordinates
into normalized coordinates. This can be done with the method
get_normalized_coordinates as illustrated in the following example:
import numpy as np
import xtrack as xt
# Load a line and build tracker
line = xt.Line.from_json(
'../../test_data/hllhc15_noerrors_nobb/line_and_particle.json')
line.particle_ref = xt.Particles(
mass0=xt.PROTON_MASS_EV, q0=1, energy0=7e12)
line.build_tracker()
# Generate some particles with known normalized coordinates
particles = line.build_particles(
nemitt_x=2.5e-6, nemitt_y=1e-6,
x_norm=[-1, 0, 0.5], y_norm=[0.3, -0.2, 0.2],
px_norm=[0.1, 0.2, 0.3], py_norm=[0.5, 0.6, 0.8],
zeta=[0, 0.1, -0.1], delta=[1e-4, 0., -1e-4])
# Inspect physical coordinates
tab = particles.get_table()
tab.show()
# prints
#
# Table: 3 rows, 17 cols
# particle_id s x px y py zeta delta chi ...
# 0 0 -0.000253245 3.33271e-06 5.10063e-05 1.00661e-06 0 0.0001 1
# 1 0 -2.06127e-09 3.32087e-07 -3.42343e-05 5.59114e-08 0.1 0 1
# 2 0 0.000152331 -7.62878e-07 3.45785e-05 1.0462e-06 -0.1 -0.0001 1
# Compute twiss
tw = line.twiss()
# Use twiss to compute normalized coordinates
norm_coord = tw.get_normalized_coordinates(particles, nemitt_x=2.5e-6,
nemitt_y=1e-6)
# Inspect normalized coordinates
norm_coord.show()
#
# Table: 3 rows, 8 cols
# particle_id at_element x_norm px_norm y_norm py_norm zeta_norm pzeta_norm
# 0 0 -1 0.1 0.3 0.5 1.06651e-07 0.00313799
# 1 0 -1.59607e-20 0.2 -0.2 0.6 0.00318676 1.12046e-05
# 2 0 0.5 0.3 0.2 0.8 -0.0031868 -0.0031492
# Complete source: xtrack/examples/twiss/012_compute_norm_coordinates.py
Reverse reference frame
The reverse` flag, allows getting the output of the twiss in the counter-rotating reference system. When reverse is True, the ordering of the elements is reversed, the zero of the s` coordinate and of the phase advances is set at the new start, the sign of the coordinates s` and x` is inverted, while the sign of the coordinate y is unchanged. This is illustrated in the following example:
import xtrack as xt
# Load collider with two lines
collider = xt.Multiline.from_json(
'../../test_data/hllhc15_thick/hllhc15_collider_thick.json')
collider.build_trackers()
collider.lhcb1.twiss_default.clear() # clear twiss default settings
collider.lhcb2.twiss_default.clear() # clear twiss default settings
collider.vars['on_disp'] = 0 # disable dispersion correction
# Set a horizontal crossing angle between the two beams in the interaction
# point ip1 and a vertical crossing angle in ip5
collider.vars['on_x1hl'] = 10 # [urad]
collider.vars['on_x5vl'] = 10 # [urad]
# Set a vertical separation between the two beams in the interaction point ip5
# and a horizontal separation in ip5
collider.vars['on_sep1v'] = 0.5 # [mm]
collider.vars['on_sep5h'] = 0.5 # [mm]
# Twiss the two lines (4d method since cavities are off)
tw1 = collider.lhcb1.twiss(method='4d')
tw2 = collider.lhcb2.twiss(method='4d')
tw1.reference_frame # is `proper`
tw2.reference_frame # is `proper`
# tw1 has a clokwise orientation while tw2 has a counter-clockwise orientation.
#
# name s mux muy x y px py
# ip1 0 0 0 4.313e-09 0.0005 1.002e-05 -4.133e-09
# ip3 6665 15.95 15.45 2.392e-08 -2.209e-07 3.695e-10 -3.005e-09
# ip5 1.333e+04 30.93 29.99 0.0005 4.332e-09 1.918e-08 1e-05
# ip7 1.999e+04 46.35 44.59 2.138e-07 -1.785e-08 -2.132e-09 -3.078e-11
tw2.rows['ip[1,3,5,7]'].cols['s mux muy x y px py'].show(digits=4)
# prints:
#
# name s mux muy x y px py
# ip7 6665 16.19 15.45 -5.941e-09 2.69e-07 -1.098e-10 2.428e-09
# ip5 1.333e+04 31.28 30.37 0.0005 5.997e-09 -4.562e-09 1.003e-05
# ip3 1.999e+04 46.46 44.81 -9.85e-08 -2.447e-08 3.218e-09 -9.711e-10
# ip1 2.666e+04 62.31 60.32 -2.278e-09 -0.0005 -1e-05 2.57e-08
# -- Reverse b2 twiss --
# The `reverse`` flag, allows getting the output of the twiss in the counter-rotating
# reference system. When `reverse` is True, the ordering of the elements is reversed,
# the zero of the s coordinate and fo the phase advances is set at the new start,
# the sign of the coordinates s and x is inverted, while the sign of the coordinate
# y is unchanged. In symbols:
#
# s -> L - s
# mux -> mux(L) - mux
# muy -> muy(L) - muy
# x -> -x
# y -> y
# px -> px
# py -> -py
tw2_r = collider.lhcb2.twiss(method='4d', reverse=True)
tw2_r.reference_frame # is `reverse`
tw2_r.rows['ip[1,3,5,7]'].cols['s mux muy x y px py'].show(digits=4)
# prints:
#
# name s mux muy x y px py
# ip1 2.183e-11 0 0 2.278e-09 -0.0005 -1e-05 -2.57e-08
# ip3 6665 15.85 15.51 9.85e-08 -2.447e-08 3.218e-09 9.711e-10
# ip5 1.333e+04 31.03 29.95 -0.0005 5.997e-09 -4.562e-09 -1.003e-05
# ip7 1.999e+04 46.12 44.87 5.941e-09 2.69e-07 -1.098e-10 -2.428e-09
# In this way, for a collider, it is possible to plot the closed orbit and the
# twiss functions of the two beams in the same graph. For example:
import matplotlib.pyplot as plt
plt.close('all')
fig = plt.figure(1)
ax1 = fig.add_subplot(211)
ax1.plot(tw1.s, tw1.x * 1000, color='b', label='b1')
ax1.plot(tw2_r.s, tw2_r.x * 1000, color='r', label='b2')
ax1.set_ylabel('x [m]')
ax1.legend(loc='best')
ax2 = fig.add_subplot(212, sharex=ax1)
ax2.plot(tw1.s, tw1.y * 1000, color='b', label='b1')
ax2.plot(tw2_r.s, tw2_r.y * 1000, color='r', label='b1')
ax2.set_ylabel('y [mm]')
ax2.set_xlabel('s [mm]')
ax1.set_xlim(tw1['s', 'ip5'] - 300, tw1['s', 'ip5'] + 300)
ax1.axvline(x=tw1['s', 'ip5'], color='k', linestyle='--', alpha=0.5)
ax2.axvline(x=tw1['s', 'ip5'], color='k', linestyle='--', alpha=0.5)
plt.text(tw1['s', 'ip5'], -0.6, 'ip5', rotation=90, alpha=0.5,
horizontalalignment='left', verticalalignment='top')
plt.show()
# Complete source: xtrack/examples/twiss/000e_twiss_reverse.py
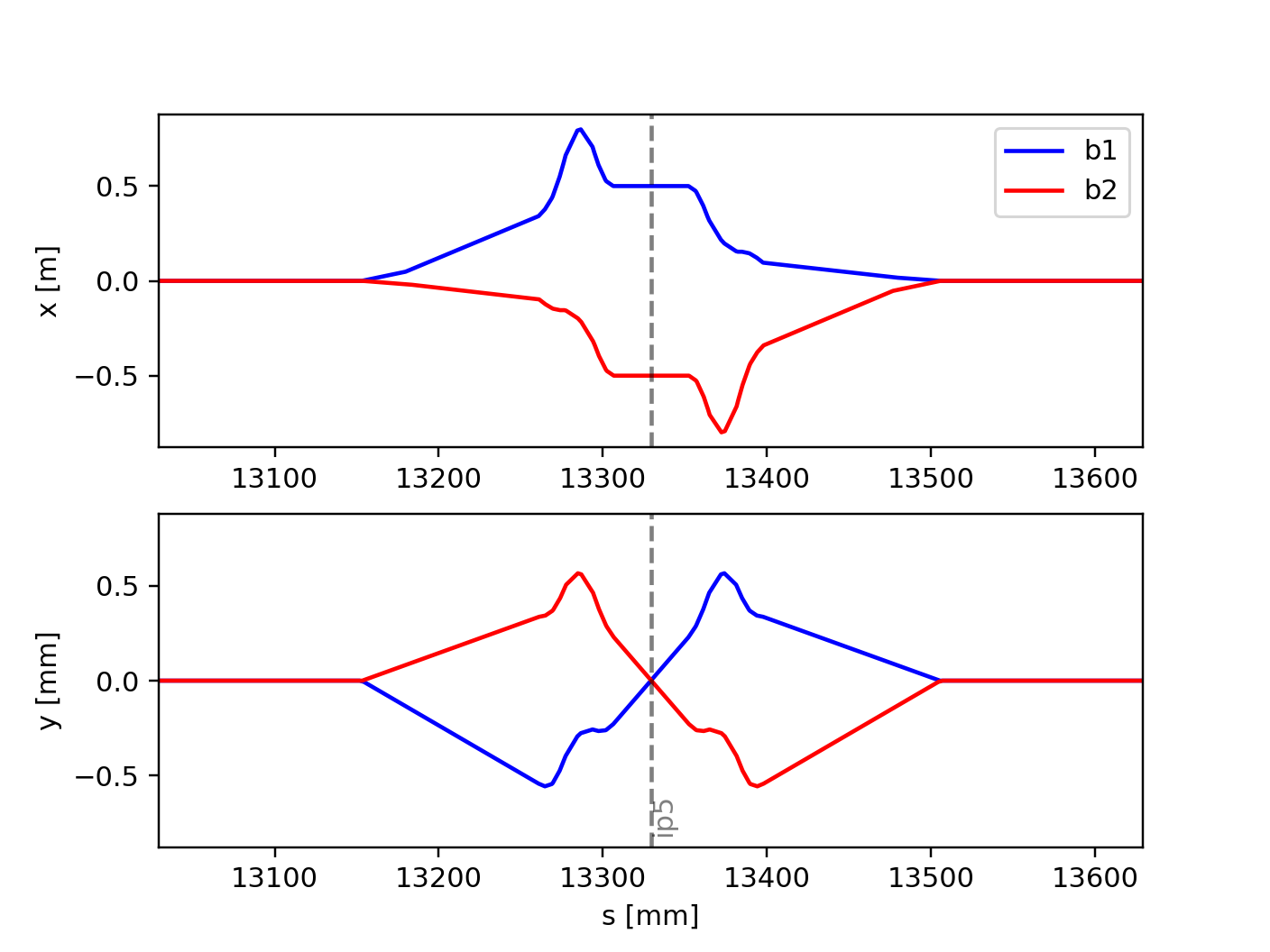
Closed Orbit of the two LHC beams in the same reference frame. This is
obtained setting reverse=True on the twiss of beam 2.
Twiss defaults
It is possible to change the default behavior of the twiss method for a given
line using line.twiss_defaults, which is a dictionary with the desired
default twiss arguments. This is illustrated in the following example:
import xtrack as xt
# Load a line and build tracker
line = xt.Line.from_json(
'../../test_data/hllhc15_noerrors_nobb/line_and_particle.json')
line.particle_ref = xt.Particles(mass0=xt.PROTON_MASS_EV, q0=1, energy0=7e12)
line.build_tracker()
# Twiss (built-in defaults)
tw_a = line.twiss()
tw_a.method # is '6d'
tw_a.reference_frame # is 'proper'
# Inspect twiss defaults
line.twiss_default # is {}
# Set some twiss defaults
line.twiss_default['method'] = '4d'
line.twiss_default['reverse'] = True
# Twiss (defaults redefined)
tw_b = line.twiss()
tw_b.method # is '4d'
tw_b.reference_frame # is 'reverse'
# Inspect twiss defaults
line.twiss_default # is {'method': '4d', 'reverse': True}
# Reset twiss defaults
line.twiss_default.clear()
# Twiss (defaults reset)
tw_c = line.twiss()
tw_c.method # is '6d'
tw_c.reference_frame # is 'proper'
# Complete source: xtrack/examples/twiss/000f_twiss_default.py